Straumlinje
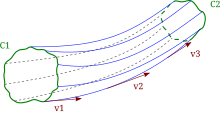
Dei tjukke blå linjene og stipla grå linjene representerer straumlinjer. Den raude pila syner retninga og storleiken til snøggleiken til straumen. Desse pilene er tangentar til straumlinjene. Straumlinjene går mellom dei grøne kurvene (C1{displaystyle C_{1}} og C2{displaystyle C_{2}}) og dannar ei straumflate.
Straumlinjer er kurver der snøggleiksvektoren er tangent til kvart punkt på kurva. Desse syner retninga eit væskeelement vil flytte seg i for alle tidspunkt.
Straumlinjer er definerte som[1]
- dx→Sds×u→(x→S)=0,{displaystyle {d{vec {x}}_{S} over ds}times {vec {u}}({vec {x}}_{S})=0,}
der «×» er vektor-kryssproduktet og x→S(s){displaystyle {vec {x}}_{S}(s)} er den parametrisk representasjon av berre ei straumlinje ved eit vilkårleg tidspunkt.
Om snøggleikskomponenten vert skriven u→=(u,v,w),{displaystyle {vec {u}}=(u,v,w),} og dei for straumlinjene vert skriven x→S=(xS,yS,zS),{displaystyle {vec {x}}_{S}=(x_{S},y_{S},z_{S}),} finn vi:[1]
- dxSu=dySv=dzSw,{displaystyle {dx_{S} over u}={dy_{S} over v}={dz_{S} over w},}
som syner at kurvene er parallelle til snøggleiksvektoren. Her er s{displaystyle s} variabel som parametriserer kurva s↦x→S(s).{displaystyle smapsto {vec {x}}_{S}(s).}
Kjelder |
Denne artikkelen bygger på «Streamlines, streaklines, and pathlines» frå Wikipedia på engelsk, den 20. august 2010.
- Wikipedia på engelsk oppgav desse kjeldene:
Faber, T.E. (1995). Fluid Dynamics for Physicists. Cambridge University Press. ISBN 0-521-42969-2.
↑ 1,01,1 Granger, R.A. (1995). Fluid Mechanics. Dover Publications. ISBN 0486683567. , s. 422–425.
- NPTEL web content








